Question

Evaluate the function requested. Write your answer as a fraction in lowest terms. Triangle A B C. Angle C is 90 degrees. Hypotenuse A B is 35, side C B is 28, side C A is 21. Find sin A. a. Sine A = four-thirds c. sine A = three-fifths b. sine A = four-fifths d. sine A = five-fourths

Answer 1

its B 4/5

Explanation:

Answer 2

sine A = four-fifths

Explanation:

You have a rectangle triangle ABC with hypotenuse AB 35, side CB 28 and side CA 21. The angle C is 90°.

In order to calculate sin A, you take into account that:

`sinA=(opposite\ side\ to\ A)/(hypotenuse)`

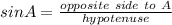
The opposite side to angle A is side CB = 28

Hypotenuse = 35

You replace the numeric values of the hypotenuse and side BC in the formula for sinA:

`sinA=(28)/(35)`

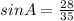
In order to simply the fraction, you divide both numerator and denominator by 7:

`sinA=(28/7)/(35/7)=(4)/(5)`

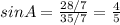
hence, the answer is

sine A = four-fifths