Question

uppose that​ Mary's utility function is​ U(W) = W0.5​, where W is wealth. She has an initial wealth of​ $100. How much of a risk premium would she want to participate in a gamble that has a​ 50% probability of raising her wealth to ​$115 and a​ 50% probability of lowering her wealth to ​$77​? ​Mary's risk premium is ​$ nothing. ​ (round your answer to two decimal places​)

Answer 1

Note that
`U(W) = W^(0.5)`

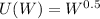
Answer:

Mary's risk premium is $0.9375

Explanation:

Mary's utility function,
`U(W) = W^(0.5)`

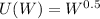
Mary's initial wealth = $100

The gamble has a 50% probability of raising her wealth to $115 and a 50% probability of lowering it to $77

Expected wealth of Mary,
`E_w`

`E_(w)` = (0.5 * $115) + (0.5 * $77)

`E_(w)` = 57.5 + 38.5

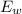`E_(w)` = $96

The expected value of Mary's wealth is $96

Calculate the expected utility (EU) of Mary:-

`E_u = [0.5 * U(115)] + [0.5 * U(77)]\\E_u = [0.5 * 115^(0.5)] + [0.5 * 77^(0.5)]\\E_u = 5.36 + 4.39\\E_u = \$ 9.75`

The expected utility of Mary is $9.75

Mary will be willing to pay an amount P as risk premium to avoid taking the risk, where

U(EW - P) is equal to Mary's expected utility from the risky gamble.

U(EW - P) = EU

U(94 - P) = 9.63

Square root (94 - P) = 9.63

If Mary's risk premium is P, the expected utility will be given by the formula:

`E_(u) = U(E_(w) - P)\\E_(u) = U(96 - P)\\E_u = (96 - P)^(0.5)\\(E_u)^2 = 96 - P\\ 9.75^2 = 96 - P\\95.0625 = 96 - P\\P = 96 - 95.0625\\P = 0.9375`

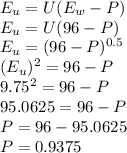
Mary's risk premium is $0.9375