Question

Your friend asks you to help him study and will pay you 5 dimes the first time you help him. You agree to help if he multiplies your payment by 5 for each study session. After 2 study sessions, you will receive 25 dimes, and after 3 study sessions, you will receive 125 dimes.

Complete and solve the equation that finds the number of dimes he will pay you after the 7th study session.

Answer 1

`a_7=5(5)^(6)`

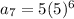
78125 dimes

Explanation:

The given scenario can be modeled as a geometric sequence.

A geometric sequence has a common ratio (multiplier) between each term, so each term is multiplied by the same number.

General form of a geometric sequence:

`a_n=ar^(n-1)`

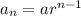
where:

• n is the nth term
• a is the first term
• r is the common ratio

Given:

• The friend will pays 5 dimes the first time you help him.

Therefore, a = 5

Given:

• The friend multiplies your payment by 5 for each study session.

Therefore, r = 5

Substitute these values into the formula to create an equation for the nth term.

`\implies a_n=5(5)^(n-1)`

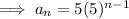
To find the number of dimes he will pay after 7 sessions, simply substitute n = 7 into the found equation:

`\implies a_7=5(5)^(7-1)`

`\implies a_7=5(5)^(6)`

`\implies a_7=5 \cdot 15625`

`\implies a_7=78125`

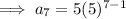
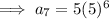
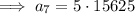
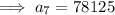
Therefore, the friend will pay 78125 dimes after the 7th study session.

Answer 2

• 78125 dimes

Explanation:

The payment for sessions makes a series

• 5 dimes, 5*5 = 25 dimes, 25*5 = 125 dimes, ...

This series is GP with the first term of 5 and common ratio of 5.

The nth term would be

• 
  `t_n=5*5^(n-1)`

Use the equation above and find the 7th term

• 
  `t_7=5*5^6 = 5^7 = 78125`