Question

According to a study conducted in 2015, 18% of shoppers said that they prefer to buy generic instead of name-brand products. Suppose that in a recent sample of 1500 shoppers, 315 stated that they prefer to buy generic instead of name-brand products. At a 5% significance level, can you conclude that the proportion of all shoppers who currently prefer to buy generic instead of name-brand products is higher than .18? Use both the p-value and the critical-value approaches.

Answer 1

There is evidence to said that the proportion of all shoppers who currently prefer to buy generic instead of name-brand products is higher than 0.18

Explanation:

First, we need to define the null and alternative hypothesis as:

H0: p = 0.18

H1: p > 0.18

Where p is the proportion of shoppers that said that they prefer to buy generic instead of name-brand products.

Then, we can calculated the test statistic using the following equation:

`z=\frac{p'-p}{\sqrt{(p(1-p))/(n) } }`

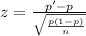
Where p' is the proportion of the sample and n is the size of the sample.

Replacing p by 0.18, p' by 0.21 (315/1500 = 0.21) and n by 1500, we get:

`z=\frac{0.21-0.18}{\sqrt{(0.18(1-0.18))/(1500) } }=3.02`

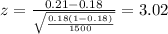
So, using the standard normal table, the p-value is calculated as:

p-value = P(z>3.02) = 0.0013

Additionally, At a 5% significance level, the critical value is the z value that let 5% on the right tail, so it is calculated as:

P(Z>z) = 0.05

Critical Value = 1.64

Finally, taking into account that the 5% significance level is higher than the p-value and the critical value is higher than the test statistic, we reject the null hypothesis and there is evidence to said that the proportion of all shoppers who currently prefer to buy generic instead of name-brand products is higher than 0.18