Question

A​ person's blood pressure is monitored by taking 8 readings daily. The probability distribution of his reading had a mean of 129 and a standard deviation of 7. a. Each observation behaves as a random sample. Find the mean and the standard deviation of the sampling distribution of the sample mean for the eight observations each day. b. Suppose that the probability distribution of his blood pressure reading is normal. What is the shape of the sampling​ distribution? c. Refer to​ (b). Find the probability that the sample mean exceeds 140.

Answer 1

a)
`\mu_(\bar X)= 129`

`\sigma_(\bar X)= (7)/(√(8))=2.475`

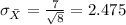
b) If the distribution is normal then the sampling distribution would be bell shaped and normal

c)
`P(\bar X >140)`

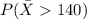
And we can use the z score formula given by:

`z =(\bar X -\mu)/(\sigma_(\bar X))`

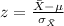
And replacing we got:

`z =(140-129)/(2.475)= 4.44`

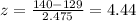
And then we can find the probability using the complement rule and the normal standard distribution or excel and we got:

`P(\bar X>140) = P(Z>4.44) =1-P(z<4.44) \approx 0`

Explanation:

For this case we have the following info:

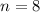`n=8` represent the sample size

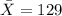`\bar X=129` the sample mean

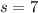`s=7` the standard deviation

Part a

If we assume that the distirbution is bell shaped then we can find the parameters like this:

`\mu_(\bar X)= 129`

`\sigma_(\bar X)= (7)/(√(8))=2.475`

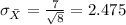
Part b

If the distribution is normal then the sampling distribution would be bell shaped and normal

Part c

We want this probability:

`P(\bar X >140)`

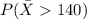
And we can use the z score formula given by:

`z =(\bar X -\mu)/(\sigma_(\bar X))`

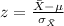
And replacing we got:

`z =(140-129)/(2.475)= 4.44`

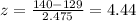
And then we can find the probability using the complement rule and the normal standard distribution or excel and we got:

`P(\bar X>140) = P(Z>4.44) =1-P(z<4.44) \approx 0`