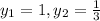Answer:
i)
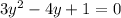
We can divide both sides of the equation by 3 and we got:
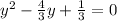
Now we can complete the square and we got:
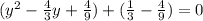

We take square root on both sides and we got:

And the solutions for y are:
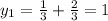
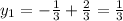
ii)
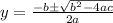
And with
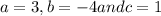 we got:
we got:
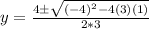
And we got:
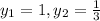
Explanation:
Part i
For this case we have the following function given:
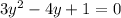
We can divide both sides of the equation by 3 and we got:
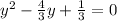
Now we can complete the square and we got:
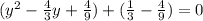

We take square root on both sides and we got:

And the solutions for y are:
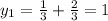
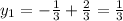
Part ii
We can use the quadratic formula:
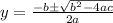
And with
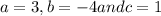 we got:
we got:
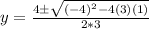
And we got: