Question

Do bonds reduce the overall risk of an investment portfolio? Let x be a random variable representing annual percent return for Vanguard Total Stock Index (all stocks). Let y be a random variable representing annual return for Vanguard Balanced Index (60% stock and 40% bond). For the past several years, we have the following data.

x: 17 0 17 28 28 27 29 −12 −12 −13
y: 14 −2 27 18 20 11 14 −2 −3 −10
A) Compute ∑x, ∑x2, ∑y, ∑y2
B) Use the results of part (a) to compute the sample mean, variance, and standard
deviation for x and for y.
C) Compute a 75% Chebyshev interval around the mean for x values and also for
y values. Use the intervals to compare the two funds.
D) Compute the coefficient of variation for each fund. Use the coefficients of variation
to compare the two funds. If s represents risks and image from custom entry tool represents expected return, then image from custom entry tool can be thought of as a measure of risk per unit of expected return. In this case, why is a smaller CV better? Explain.

Answer 1

a.

∑x=109, ∑x²=4173, ∑y=87, ∑y²=2083.

b.

sample mean for x=10.9.

variance for x=331.66.

standard deviation for x=18.21.

sample mean for y=8.7.

variance for y=147.34.

standard deviation for y=12.14.

c.

75% Chebyshev interval around the mean for x values

-25.52,47.32

75% Chebyshev interval around the mean for y values

-15.58,32.98

The interval shows that Vanguard Balanced index has smaller spread.

d.

coefficient of variation for x=167.06%

coefficient of variation for y=139.54%

Smaller CV means lower risk so, smaller CV is better.

Explanation:

Note: ALL ANSWERS ARE ROUNDED TO TWO DECIMAL PLACES

a.

∑x=17+0+17+28+28+27+29−12−12−13=109,

∑x²=17²+0²+17²+28²+28²+27²+29²+(−12)²+(−12)²+(−13)²=4173,

∑y=14−2+27+18+20+11+14−2−3−10=87,

∑y²=14²+(−2)²+(27)²+(18)²+(20)²+(11)²+(14)²(−2)²+(−3)²+(−10)²=2083.

b.

sample mean for x=∑x/n=109/10=10.9.

`variance x=(sum(x-mean )^2)/(n-1)`

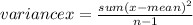
x-mean

6.10

-10.90

6.10

17.10

17.10

16.10

18.10

-22.90

-22.90

-23.90

sum(x-mean)²=6.10 ²+(-10.90 )²+6.10 ²+17.10² +17.10²+ 16.10² +18.10² +(-22.90 )²+(-22.90 )²+(-23.90 )²=2984.9

`variance x=(2984.9)/(9)`

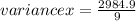
Variance for x=331.66.

standard deviation for x=√variance for x

standard deviation for x=√331.66

standard deviation for x=18.21.

sample mean for y=∑y/n=87/10=8.7.

`variance y=(sum(y-mean )^2)/(n-1)`

y-mean

5.30

-10.70

18.30

9.30

11.30

2.30

5.30

-10.70

-11.70

-18.70

sum(y-mean)²=5.30 ²+(-10.70 )²+18.30² +9.30² +11.30² +2.30² +5.30² +(-10.70 )²+(-11.70 )²+(-18.70 )²=1326.1

`variance y=(1326.1)/(9)`

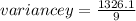
variance for y=147.34.

standard deviation for y=√variance for y

standard deviation for y=√147.34

standard deviation for y=12.14.

c.

75% Chebyshev Interval

mean±k standard deviation

We have to find value of k.

`1-(1)/(k^(2) ) =0.75`

`1-0.75 =(1)/(k^(2) )`

`(1)/(k^(2) )=0.25`

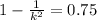
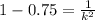
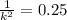
k²=4

k=2

so, 75% Chebyshev Interval for x

10.9±2*(18.21)

[-25.52,47.32]

75% Chebyshev Interval for y

8.7±2*(12.14)

[-15.58,32.98]

The interval shows that Vanguard Balanced index has smaller spread.

d.

`CV for x=(S.Dx)/(meanx) *100`

`CV for x=(18.21)/(10.9) *100`

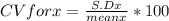
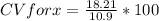
CV for x=167.06%

CV for y

`CV for y=(S.Dy)/(meany) *100`

`CV for y=(12.14)/(8.7) *100`

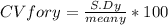
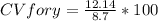
Cv for y=139.54%

The smaller CV shows the smaller amount of risk so, smaller CV is better.