Question

A long glass rod A is initially at 22.0°C. A second rod B is identical to rod A and has the same mass and initial temperature as A. The same amount of heat is supplied to both rods and the two rods A and B reach final temperatures of 86.3°C and 190.0°C respectively. If the specific heat of glass is 0.2007 kcal/(kg· °C), what is the specific heat of the material from which rod B is made?

Answer 1

`c_B=0.0768(kcal)/(kg\cdot\°C)`

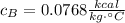
Step-by-step explanation:

In order to calculate the specific heat of the material B, you use the following formula for the change in the temperature of a substance, where an amount of heat Q is given to the substance:

`Q=mc(T_2-T_1)`

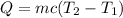
Q: amount oh heat

m: mass of the substance

T2: final temperature

T1: initial temperature

c: specific heat of the substance.

If QA and QB are the heat of material A and B, you have:

`Q_A=m_Ac_A(T_(2A)-T_(1A))\\\\Q_B=m_Bc_B(T_(2B)-T_(1B))`

both materials have the same mass, mA = mB

cA: specific heat of A = 0.2007 kcal/(kg.°C)

cB: specific heat of B = ?

T2A: final temperature of A = 86.3°C

T1A: initial temperature of A = 22.0°C

T2B: final temperature of B = 190.0°C

T1B: initial temperature of B = 22.0°C

In this case you have that both material A and B receive the same amount of heat Q. Then, you equal QA with QB and solve for cB:

`m_Ac_A(T_(2A)-T_(1A))=m_Bc_B(T_(2B)-T_(1B))\\\\c_B=(c_A(T_(2A)-T_(1A)))/((T_(2B)-T_(1B)))\\\\c_B=((0.2007kcal/(kg.\°C))(86.3\°C-22.0\°C))/(190.0\°C-22.0\°C)\\\\c_B=0.0768(kcal)/(kg\cdot\°C)`

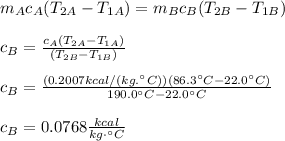
hence, the specific heat of the second rod B is 0.0768kcal/(kg°C)