Question

determine the slope of the tangent to the curve at the point y=(3x)(sinx) at the point with x-coordinate pi/2 ​

Answer 1

Explanation:

The slope of the tangent to a curve is the derivative of the curve. We need to find the derivative of the function and then evaluate the derivative at that given x value. The derivative is found using the product rule:

`y'=f(x)g'(x)+f'(x)g(x)`

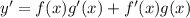
Let's call 3x our f(x) and sin(x) our g(x). Filling in the formula for the derivative using the product rule looks like this:

`y'=3x(cosx)+3sinx`

That gives us the derivative, which is the slope formula that can be used at ANY x value anywhere on the curve to find the slope of the line tangent to the curve at that x value. If we want to find the slope of the tangent line to the curve at x = pi/2, we evaluate the slope formula at x = pi/2 (remember that y' is the same exact thing as the slope):

`y'(slope)=3((\pi)/(2))(cos(\pi)/(2))+3(sin(\pi)/(2))`

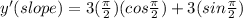
From the unit circle (or experience, since you're in advaced math), we know that the cosine of pi/2 is 0 and that the sin of pi/2 = 1:

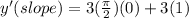`y'(slope)=3((\pi)/(2))(0)+3(1)` simplifies to

y' (slope) = 3

That means that the slope of the line tangent to the curve at the point x = pi/2 is 3.