Question

Given the data shown below, which of the following is the best prediction for

the number of years it will take for the population to reach 200,000?
Year
Population
11,920
2
16,800
3
23,300
4
33,000
5
45,750
6
64,000
O A. 9.41
O B. 12.45
O C. 15.82
O D. 18.14

Answer 1

The best prediction for the number of years it will take for the population to reach 200,000 is 9.41

Explanation:

Year Population

1 11,920

2 16,800

3 23,300

4 33,000

5 45,750

6 64,000

`y_1 =A _0 e ^(kt _1)\\y_2 = A_0 e^(k t_2)\\(t_1,y_1)=(1,11920)\\(t_2,y_2)=(2,16800)`

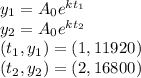
Substitute the values

`11920=A _0 e ^(k) ---1\\16800 = A_0 e^(2k) ---2`

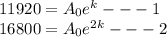
Divide 1 and 2

`(11920)/(16800)=(e^k)/(e^(2k))\\(11920)/(16800)=e^(k-2k)\\ln((11920)/(16800))=-k\\k=-1 ln((11920)/(16800))\\k=0.3432\\A_0=y_1 e^(-k t_1)\\A_0=11920 e^(-0.3432)\\A_0=8457.5238`

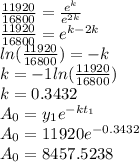
The exponential function that passes through the points (1, 11920) and (2, 16800) is
`y=8457.5238 e^(0.3432t)`

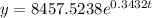
Now we are supposed to find the best prediction for the number of years it will take for the population to reach 200,000

`200000=8457.5238 e^(0.3432t)`

`(200000)/(8457.5238)=e^(0.3432t)`

`ln((200000)/(8457.5238))=0.3432t`

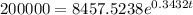
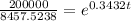
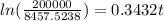
t = 9.41

Hence the best prediction for the number of years it will take for the population to reach 200,000 is 9.41