Question

Find the mean median mode and range for the following data 77 60 59 70 89 95

Answer 1

Mean = 75

Median = 73.5

Mode = 95

Range = 36

Explanation:

Given:

• 77,60,59,70,89,95

Sort:

• 59,60,70,77,89,95

To find:

• Mean
• Median
• Mode
• Range

Mean:

`\displaystyle \large{(1)/(n)\sum_(i =1)^n x_i = (x_1+x_2+x_3+...+x_n)/(n)}`

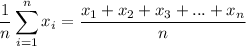
Sum of all data divides by amount.

`\displaystyle \large{(59+60+70+77+89+95)/(6)=(450)/(6)}\\\\\displaystyle \large{\therefore mean=75}`

Therefore, mean = 75

Median:

If it’s exact middle then that’s the median. However, if two data or values happen to be in middle:

`\displaystyle \large{(x_1+x_2)/(2)}`

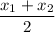
From 59,60,70,77,89,95, since 70 and 77 are in middle:

`\displaystyle \large{(70+77)/(2) = (147)/(2)}\\\displaystyle \large{\therefore median = 73.5}`

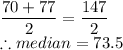
Therefore, median = 73.5

Mode:

The highest value or/and the highest amount of data. Mode can have more than one.

From sorted data, there are no repetitive data nor same data. Consider the highest value:

Therefore, mode = 95

Range:

`\displaystyle \large{x_(max)-x_(min)}` or highest value - lowest value

Thus:

`\displaystyle \large{95-59 = 36}`

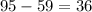
Therefore, range = 36