Answer:
This is the angle in the angle in the fourth quadrant that verifies the given conditions:
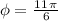
Explanation:
Notice that in the unit circle, if sin of the angle is negative, and cos of the same angle is positive, we are in the fourth quadrant.
Also, the angle that renders
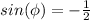
in the fourth quadrant, is
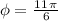
for such angle, also :
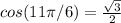
which verifies the second condition.