Answer:
0.69
Explanation:
In a right triangle, the cosine of one of the acute angles is the ratio of the adjacent ("next to") side to the hypotenuse.
In this triangle, the side adjacent to angle T has length
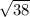 . Now you need the length of the hypotenuse, ST. Use the Pythagorean Theorem:
. Now you need the length of the hypotenuse, ST. Use the Pythagorean Theorem:
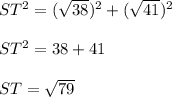
Build the ratio (adjacent) / (hypotenuse) and approximate it with a decimal.
