Answer:
Maximum revenue is 11200 at price p=10.
Explanation:
If a quadratic function is defined by
 and a<0, then it is maximum at
and a<0, then it is maximum at
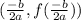 .
.
The revenue model of a company is

Here,
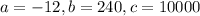 .
.
So,
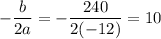
It means, revenue is maximum at price 10.
Substitute p=10 in the revenue function.
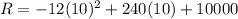
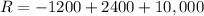
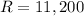
Therefore, maximum revenue is 11200 at price p=10.