Question

I run a book club with $n$ people, not including myself. Every day, for $365$ days, I invite five members in the club to review a book. What is the smallest positive integer $n$ so that I can avoid ever having the exact same group of five members over all $365$ days?

Answer 1

Explanation:

if we have n people and we want to do groups of 5, the total number of different combinations is:

`c = (n!)/((n - 5)!5!)`

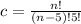
find the smallest n such c > 365.

let's do it by brute force:

if n = 5, we have:

`c = 5C_5 = 5`

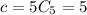
if n = 6

`c =6C_5 =6`

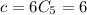
if n = 7

`c = 7C_ 5= 21`

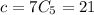
if n = 8

`c = 8C_5 = 56`

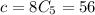
if n = 9

`C = 9!/(4!*5!) = 126`

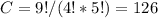
so 9 is not enough, let's see N = 10

C = 10!/(5!*5!) = 252

10 is not enough, let's see with 11.

C = 11!/(6!*5!) = 462

So you need at least 11 members in the club.

Then the minimum number of members such we have more than 365 combinations is 11 members