Question

In October 2012, Apple introduced a much smaller variant of the Apple iPad, known as the iPad Mini. Weighing less than 11 ounces, it was about 50% lighter than the standard iPad. Battery tests for the iPad Mini showed a mean life of 10.25 hours (The Wall Street Journal, October 31, 2012). Assume that battery life of the iPad Mini is uniformly distributed between 8.5 and 12 hours.

a. What is the probability that the battery life for an iPad Mini will be 10 hours or less (to 4 decimals)?b. What is the probability that the battery life for an iPad Mini will be at least 11 hours (to 4 decimals)?c. What is the probability that the battery life for an iPad Mini will be between 9.5 and 11.5 hours (to 4 decimals)?d. In a shipment of 100 iPad Minis, how many should have a battery life of at least 9 hours (to nearest whole value)?

Answer 1

a) 0.4286 = 42.86% probability that the battery life for an iPad Mini will be 10 hours or less

b) 0.2857 = 28.57% probability that the battery life for an iPad Mini will be at least 11 hours

c) 0.5714 = 57.14% probability that the battery life for an iPad Mini will be between 9.5 and 11.5 hours

d) 86 should have a battery life of at least 9 hours.

Explanation:

An uniform probability is a case of probability in which each outcome is equally as likely.

For this situation, we have a lower limit of the distribution that we call a and an upper limit that we call b.

The probability that we find a value X lower than x is given by the following formula.

`P(X \leq x) = (x - a)/(b-a)`

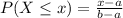
The probability of being higher than x is:

`P(X > x) = (b - x)/(b-a)`

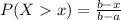
The probability of being between c and d is:

`P(c \leq X \leq d) = (d-c)/(b-a)`

Assume that battery life of the iPad Mini is uniformly distributed between 8.5 and 12 hours.

This means that
`a = 8.5, b = 12`

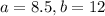
a. What is the probability that the battery life for an iPad Mini will be 10 hours or less (to 4 decimals)?

`P(X \leq x) = (x - a)/(b-a)`

`P(X \leq 10) = (10 - 8.5)/(12 - 8.5) = 0.4286`

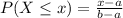
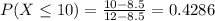
0.4286 = 42.86% probability that the battery life for an iPad Mini will be 10 hours or less.

b. What is the probability that the battery life for an iPad Mini will be at least 11 hours (to 4 decimals)?

`P(X > x) = (b - x)/(b-a)`

`P(X > 11) = (12 - 11)/(12 - 8.5) = 0.2857`

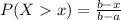
0.2857 = 28.57% probability that the battery life for an iPad Mini will be at least 11 hours

c. What is the probability that the battery life for an iPad Mini will be between 9.5 and 11.5 hours (to 4 decimals)?

`P(c \leq X \leq d) = (d-c)/(b-a)`

`P(9.5 \leq X \leq 11.5) = (11.5 - 9.5)/(12 - 8.5) = 0.5714`

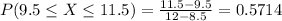
0.5714 = 57.14% probability that the battery life for an iPad Mini will be between 9.5 and 11.5 hours.

d. In a shipment of 100 iPad Minis, how many should have a battery life of at least 9 hours (to nearest whole value)?

Proportion of iPad Minis with a battery life of at least 9 hours.

`P(X > 11) = (12 - 9)/(12 - 8.5) = 0.8571`

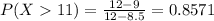
Out of 100:

0.8571*100 = 85.71

To the nearest whole number

86 should have a battery life of at least 9 hours.