Question

A 3-ton Toyota land cruiser travelled at a speed of 45m/s, collides with a 2- ton comfort taxi which was parked in front of the traffic lights intersection. After the collision, both cars lock together and move off in one direction. Determine the speed of cars after collision.

Answer 1

v = 27 m/s

Step-by-step explanation:

To find the speed of cars after the collision you take into account the momentum conservation law. Total momentum of both cars before the collision must be equal to the total momentum of both cars after the collision.

After the collision both cars traveled together, then you have:

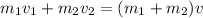`m_1v_1+m_2v_2=(m_1+m_2)v` (1)

m1: mass of the Toyota = 3-ton = 3000 kg

m2: mass of the taxi = 2-ton = 2000kg

v1: speed of the Toyota before the collision = 45m/s

v2: speed of the car before the collision = 0 m/s (it is at rest)

v: speed of both cars after the collision = ?

You solve the equation (1) for v:

`v=(m_1v_1+m_2v_2)/(m_1+m_2)`

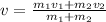
Next, you replace the values of the rest of the variables:

`v=((3000kg)(45m/s)+0kgm/s)/(3000kg+2000kg)=27(m)/(s)`

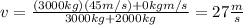
hence, just after the collision both cars have a speed of 27m/s