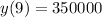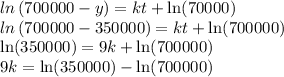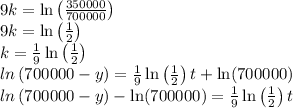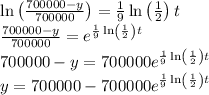Answer:
(a)
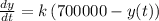
(b)
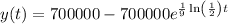
Explanation:
Given: News spreads through a city of fixed size of 700000 people at a time rate proportional to the number of people who have not heard the news.
To find:
(a) a differential equation
(b) number of people who have heard the news after t days
Solution:
(a)
Total number of people in a city = 700000
As y(t) denotes the number of people who have heard the news t days after it has happened
Number of people who have not heard the news = 700000 - y(t)
So, differential equation is
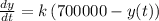
Here, k is the proportionality constant.
(b)
Integrate both sides of the differential equation.
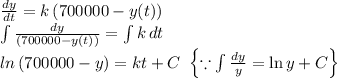
Use
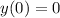
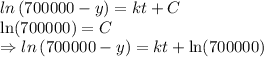
As a poll showed that 350000 people have heard the news 9 days after a scandal in City Hall was reported,