Answer:
(a) Probability that sample mean lies between 79 and 81 is 0.9946.
(b) It is 0.04% likely is it that the sample mean diameter exceeds 81 when n = 36.
Explanation:
We are given that metal sheets of a particular type, its mean value and standard deviation are 80 GPA and 1.8 GPA, respectively.
Suppose the distribution is normal.
Let
 = sample mean diameter
= sample mean diameter
The z-score probability distribution for sample mean is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 80 GPA
= population mean = 80 GPA
 = standard deviation = 1.8 GPA
= standard deviation = 1.8 GPA
n = sample size = 25
(a) Probability that sample mean lies between 79 and 81 is given by = P(79 <
 < 81) = P(
< 81) = P(
 < 81) - P(
< 81) - P(

 79)
79)
P(
 < 81) = P(
< 81) = P(
 <
<
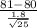 ) = P(Z < 2.78) = 0.9973
) = P(Z < 2.78) = 0.9973
P(

 79) = P(
79) = P(


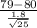 ) = P(Z
) = P(Z
 -2.78) = 1 - P(Z < 2.78)
-2.78) = 1 - P(Z < 2.78)
= 1 - 0.9973 = 0.0027
The above probability is calculated by looking at the value of x = 2.78 in the z table which has an area of 0.9973.
Therefore, P(79 <
 < 81) = 0.9973 - 0.0027 = 0.9946.
< 81) = 0.9973 - 0.0027 = 0.9946.
(b) Probability that the sample mean diameter exceeds 81 when n = 36 is given by = P(
 > 81)
> 81)
P(
 > 81) = P(
> 81) = P(
 >
>
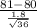 ) = P(Z > 3.33) = 1 - P(Z < 3.33)
) = P(Z > 3.33) = 1 - P(Z < 3.33)
= 1 - 0.9996 = 0.0004
The above probability is calculated by looking at the value of x = 3.33 in the z table which has an area of 0.9996.
Hence, it is 0.04% likely is it that the sample mean diameter exceeds 81 when n = 36.