Question

I. Choose the correct answer from the given alternatives

1. Which of the following is not an identity?

A. Sin2 + Cos2 = 1

B. Sin = tan.cos

C. 1 + cot2= cos2

D. 1 – sec2 = tan2

2. The exact value of cot (-8550) is ________?

A. 2 B. 1 C. -1 D. 0

3. Which one of the following is necessarily true?

A. Any rectangle is a square

B. Any rhombus is a square

C. Any square is a rectangle

D.Any a parallelogram is a rhombus

4. If the two diagonals of the quadrilateral bisect each other, then

the quadrilateral is necessarily

A. Square B. rhombus C. parallelogram D. Rectangle

5. The angle of deperession of aPt A, as measured form the top of

abuilding 30m tall is 450, how far is A from the basc of the

building?

A. 97m B. 30m C. 45m D. 32m

6. Which of the following is negative?

A. Cos(-890)

B. Tan(-1200)

C. Sin (1200)

D.Sin (-890)

7. If 300 and 450 are respectively the angle of elevation of the foot

and the top of a television antenna on the top of 100meter tall

building then the total height of the antenna from the ground

is ______________?

A. 100√3m B. 120m C. 150m D. 120√3

8. If A(-2, 3) , B(-2, -7) and c(-4, 5) are the three vertices of a

triangle. What is the Pt at which the medians intersect?

A. (3, -3) B. (-3, 3) C. (1, -2) D. (0, -3)

9. What is the periemeter of a rhombus whose diagonal are 16

and 30 units?

B. 68 unit B. 92 unit C. 46 unit D. 42 unit

10. Which of the following can never be the mesure of each

exterior angle of regular polygon?

A. 150 B. 200 C. 250 D. 300​

Answer 1

1. C. 1 + cot²θ = cos²θ

D. 1 - sec²θ = tan²θ

2. D. 0

3. C. Any square is a rectangle

4. C. Parallelogram

5. B. 30 m

6. A. cos(-890°) is Negative

Sin(-890°) is negative

7. A. 100·√3 m

8.
`\left ((-8)/(3) , (1)/(3) \right )`

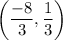
9. First option, A. 68 unit

10. A. 150

Explanation:

1. C. 1 + cot²θ = cos²θ

The correct identity is given as follows;

1 + cot²θ = csc²θ

Also

D. 1 - sec²θ = tan²θ

The correct identity is given as follows;

1 - sec²θ = -tan²θ

2. cot(-8550)

We convert -8550 to degrees by dividing by 360 and multiplying the remaining fraction by 360 as follows;

`(-8550)/(360) = -23(3)/(4)`

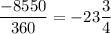
Therefore, -8550 ≅ -3/4×360 = -270

-270 ≅ 360 - 270 = 90°

Therefore, cot(-8550) = cot(90) = 1/(tan(90)) = 1/∞ = 0

Therefore, the correct option is the option D. 0

3. The correct option is any square is a rectangle as a square (a rectangle with all sides equal) is a subset of the set of rectangles

The correct option is C. Any square is a rectangle.

4. Where the diagonals bisect each other, we have a shape where the two opposite triangle areas across the bisector are equal

Therefore, the quadrilateral is necessarily a C. Parallelogram

5. Where by the angle of depression = 45°

Therefore, the angle of elevation = 45° (Alternate angles)

The height of the building = 30 m

Therefore, tan(45°) = (30 m)/(Distance of point A from the building) = 1

∴ The distance of point A from the building = 30 m

The correct option is therefore;

B. 30 m

6. A. -890° = 190° which is in the second quadrant

Therefore, cos(190°) = Negative

B. -1200° = -120° = 240 which is in the third quadrant

Hence, tan(-1200) = tan(240) is positive

C. Sin(1200) = Sin(120) which is in the second quadrant

Hence, sin(1200) is positive

D. Sin(-890°) = Sin(190°) which is in the third quadrant

Hence, sin(-890) is negative

7. The distance from the wall where the measurement is taken = 100/(tan(30)) = 100·√3 = 173.21 m

The total height of the antenna from the ground = 173.21 × tan(45) = 100·√3 m

The total height of the antenna from the ground is 100·√3 m

The correct option is therefore;

A. 100·√3 m

8. The coordinates of the point of intersection of the medians is given by the relation;

`Centroid = \left ((x_(1)+x_(2)+x_(3))/(3) , (y_(1)+y_(2)+y_(3))/(3) \right )`

Where:

x₁, y₁ x₂, y₂, x₃, y₃ are the coordinates of the vertices

We therefore have;

`Median \, point= \left (((-2) +(-2)+(-4))/(3) , (3+(-7)+5)/(3) \right ) = \left ((-8)/(3) , (1)/(3) \right )`

9. The perimeter of the rhombus = 4×√(First diagonal)/2)

`The \, perimeter \, of \, the \, rhombus = 4* \sqrt{\left ((First \, diameter)/(2) \right )^(2)+ \left ((Second \, diameter)/(2) \right )^(2)}`

`= 4* \sqrt{\left ((16)/(2) \right )^(2)+ \left ((30)/(2) \right )^(2)} = 68 \ unit`

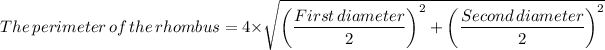
The correct option is A. 68 unit

10. The exterior angle of a regular polygon > 180°, therefore, the correct option is A. 150