Question

What is the discriminant and what does it tell us about the solutions to the quadratic? LaTeX: 3x^2+5x+4

Answer 1

The discriminant for this quadratic is -23 and tells us that there are no x-intercepts.

Explanation:

The discriminant is
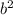`b^(2)` + 4ac; if it looks familiar, its because its underneath the square root in the quadratic equation.

The purpose of finding the discriminant is to find out:

1) if there are any x-intercepts

2) if there are, how many x-intercepts there are

When you solve for the discriminant, there are 3 types of answers you can get, here's what they mean:

1) Any negative answer - like in this quadratic graph

- this means that there are no solutions, or in other words, no x-intercepts. This means that the turning point is above the x-axis.

2) Whenever it equals 0

- this means that there is only one solution or one x-intercept for the equation.

3) Any positive answer bigger than 0.

- this means that there are 2 solutions/x-intercepts for the equation.

To find the discriminant for the quadratic 3x^2+5x+4:

Use the expression
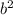`b^(2)` + 4ac, so:

*a is always the coefficient of x^2, b is always the coefficient of x and c is always the constant.

a= 3, b=5 and c=4

= (
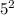`5^(2)`) - 4 x 3 x 4

= 25 - 48

= -23

Therefore, there are no solutions to this quadratic.

Hope this helped : )