Answer:
a) 13.9%.
b) If the nuber of patient files in this study were increased to 100, the margin of error would be decreased.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
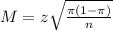
95% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
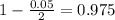 , so
, so
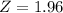 .
.
35 random patient files and finds that 27 of these patients are using this same toothpaste.
This means that
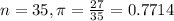
a. What is the margin of error for a 95% confidence interval to the nearest tenth of a percent?
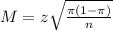
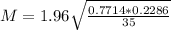
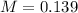
As a percent, a margin of error of 13.9%.
b. If the number of patient files in this study were increased to 100, what would happen to the margin of error?
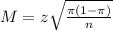
This means that the margin of error is inversely proportional to the sample size. As n increases, n decrease. Then:
If the nuber of patient files in this study were increased to 100, the margin of error would be decreased.