Question

What is one solution of the following system? StartLayout Enlarged left-brace 1st row 2 y minus 2 x = 12 2nd row x squared + y squared = 36 EndLayout (–6, 0) (–2, 4) (0, –6) (4, –2)

Answer 1

A on edge

Explanation:

Answer 2

Option A.

Explanation:

The given equations are

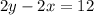`2y-2x=12` ...(1)

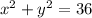`x^2+y^2=36` ...(2)

From equation (1), we get

`2y=12+2x`

`y=(12+2x)/(2)`

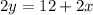
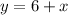`y=6+x` ...(3)

Substitute
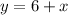`y=6+x` in equation (2).

`x^2+(6+x)^2=36`

`x^2+36+12x+x^2=36`

`2x^2+12x=0`

`2x(x+6)=0`

`x=0,-6`

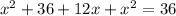
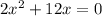
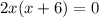
Put x=0, in equation (3).

`y=6+0=6`

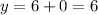
Put x=-6, in equation (3).

`y=6-6=0`

It means, (0,6) and (-6,0) are two solutions of the given system of equations.

Therefore, the correct option is A.