Answer:
Explanation:
In the figure attached,
ΔABC is an equilateral triangle,
Sides AB = BC = AC and points P, Q, and R are the midpoints of these sides respectively.
If the coordinates of A(0, 0), B(2a, 0) and C(a, b)
AB = 2a
AC =
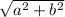
Since AB = AC
2a =
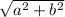
4a² = a² + b²
3a² = b²
Therefore, ordinate pairs representing midpoints of AB, BC and AC will be
P =
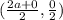 =(a, 0)
=(a, 0)
Q =
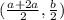 =
=

R =
 =
=
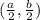
Now we will find the lengths of medians with the help of formula of distance between two points (x, y) and (x', y')
d =

AQ =
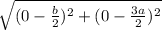
=
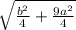
=

=
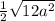 [Since b² = 3a²]
[Since b² = 3a²]
=
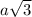
BR =
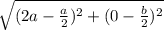
=
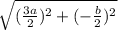
=

=

=
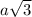
CP = b =
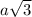
Therefore, AQ = BR = CP =
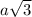
Hence, medians of an equilateral triangle are equal.