Question

Clarence wants to estimate the percentage of students who live more than three miles from the school. He wants to create a

98%
confidence interval which has an error bound of at most
4%
. How many students should be polled to create the confidence interval?

Answer 1

847 students must be interviewed.

Step-by-step explanation:

To reach this result we will use the following formula:

`n = (z^2*p*(1-p))/(e^2)`

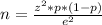
In this formula the letter "e" is equal to 0.04 (4%). Thus, we must find the values of "p" and "z", to find the "n", which refers to the confidence interval.

The question above did not show us what value should be used in "p". When we do not have information on this value, it is always recommended to use 0.5, which is the sample maximization value.

In the situation shown in the question above, a confidence interval of 98% is presented. Thus, it is implicit that we must adopt in "z" a value among the cumulative values of the z distribution of up to 1% or up to 99%. That way you can use any value between the range of 1% to 99%, you should look for that value in a table of Z, however, to facilitate the calculation we will use a value of the area of 99% in the distribution of z. This value is 2,327.

Now we can replace these values in the formula and find the value of "n".

`n = (2.327^2*0.5*(1-0.5))/(0.04^2) = 846.08`

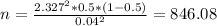
As there are no 0.8 students, we must round the number to 487. So we can say that it will be necessary to interview 847 students to create the confidence interval.