Answer:
Explanation:
Let's first have a look at the basic trigoniometric statements, which say the following:
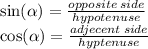
When we're looking from the point of view of angle G, we have the following data:
Since the hypotenuse is 17
adjacent is 8,
the value of the opposite is x:
Let the side be x
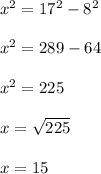
- The length of the opposite side is 15
- The length of the adjecent side is 8
- The length of the hypotenuse is 17
Now plug in this data into our general formulae.
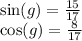
Hence, answer B. is correct.
~ Hope this helps you!