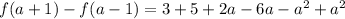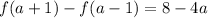Answer:
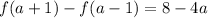
Explanation:
Given
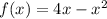
Required:

First, we solve for

This is solved by substituting a + 1 for x in f(x)
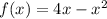 becomes
becomes
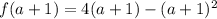
Open bracket
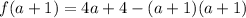
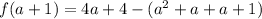
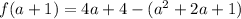
Open bracket
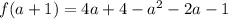
Collect like terms

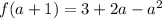
Solving for
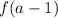
This is solved by substituting a - 1 for x in f(x)
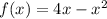 becomes
becomes
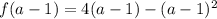
Open bracket
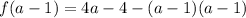
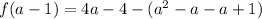

Open bracket

Collect like terms
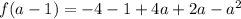
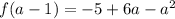
 becomes
becomes
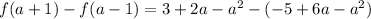
Open bracket

Collect like terms