Question

Which explicit formula can be used to model the same sequence? f(x) = 12(4)x f(x) = 3(4)x − 1 f(x) = 4(12)x f(x) = 4(3)x − 1

Answer 1

B. gives the required expression.

Explanation:

Answer 2

B.
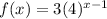`f(x) = 3(4)^(x-1)` gives the required expression.

Explanation:

The question is incomplete. Here is the complete question.

Sebastian writes the recursive formula f(x+1) = 4f(x) to represent a geometric sequence whose second term is 12. Choose the explicit formula that can be used to model the same sequence.

A.) f(x) = 12(4)x

B.) f(x) = 3(4)x − 1

C.) f(x) = 4(12)x

D.) f(x) = 4(3)x − 1

Given the recursive formula f(x+1) = 4f(x) and second term is 12 then f(2) = 12

If x =2

f(2+1) =4f(2)

f(3)= 4f(2)

f(3)= 4*12

f(3) = 48

if x = 3

f(3+1) =4f(3)

f(4)= 4f(3)

f(4)= 4*48

f(4) = 192

To get the first term, we will substitute x = 1 into the recursive function;

f(1+1) =4f(1)

f(2) = 4f(1)

since f(2) = 12 then f(2) = 4f(1) = 12

f(1) = 12/4 = 3

The sequence formed by the first four terms of recursive function is 3, 12, 48, 192... which gives a geometric sequence.

The xth term of a geometric sequence is expressed as
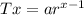`Tx = ar^(x-1)` where a is the first term and r is the common ratio.

from the sequence above a is 3 and r = 12/3 = 48/12 = 194/48 = 4

Substituting this value into the nth term of the sequence;

`Tx = 3(4)^(x-1)`

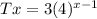
This gives the required expression.