Question

Suppose you deposit $2500 in a savings account that pays you 5% interest per year. (Calculator)

(a) How many years will it take for you to double your money?

Answer 1

14.20669 years

Roughly 14 years and 2.5 months.

Explanation:

Assuming this is compound interest.

The formula is
`A=P(1+(r)/(n))^(nt)`

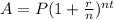
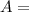`A=` Final Amount

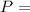`P=` Principal Amount

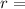`r=` Interest Rate

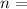`n=` # of times interest is compounded per year

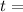`t=` Time in years

We are looking for the times in years to double the money so

`2500*2=5000`

`A=5000`

`P=2500`

`r=0.05`

`n=1`

`t=?`

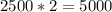
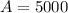
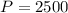
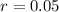
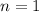
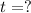
Lets solve for
`t` .

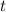Step 1.

Plug in our numbers into the compound interest formula.

`5000=2500(1+(0.05)/(1)) ^(1*t)`

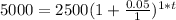
Step 2.

Simplify the equation.

Evaluate
`1+(0.05)/(1)=1.05`

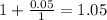
Evaluate
`1*t=t`

`5000=2500(1.05) ^(t)`

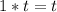
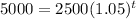
Step 3.

Divide both sides of the equation by
`2500`

`(5000)/(2500)=1.05 ^(t)`

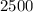
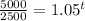
Evaluate
`(5000)/(2500)=2`

`2=1.05 ^(t)`

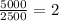
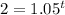
Step 4.

Take the natural log of both sides of the equation and rewrite the right side of the eqaution using properties of exponents/logarithms.

`ln(2)=t*ln(1.05)`

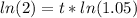
Step 5.

Divide both sides of the equation by
`ln(1.05)`

`(ln(2))/(ln(1.05))=t`

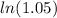
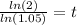
Step 6.

Evaluate

`t=14.20669`

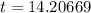
Roughly 14 years and 2.5 months.