Question

The line whose equation is 3x - 5y = 4 is dilated by a scale factor of 3

centered at the origin. Which statement is correct? *​

Answer 1

Answer 1.

Explanation:

The complete question is:

The line whose equation is 3x - 5y = 4 is dilated by a scale factor of 3 centered at the origin. Which statement is correct?

1. The image of the line has the same slope as the pre-image but a different y-intercept.

2. The image of the line has the same y-intercept as the pre-image but a different slope.

3. The image of the line has the same slope and the same y-intercept as the pre-image.

4. The image of the line has a different slope and a different y-intercept from the pre-image.

Recall that a dilation by a scale factor r centered at the origin takes a point (x,y) and maps it to the point (r*x,r*y).

Consider also a line of equation
`ax+by=c`. From this equation, the slope of the line is given by the number
`(-a)/(b)` and the y-intercept is given by
`(c)/(b)`.

Consider the given equation 3x-5y =4. If we replace (x,y) with (3x,3y), we get

`3(3x)-5(3y) = 4 = 3 (3x-5y) = 4`

which is equivalent to

`3x-5y = (4)/(3)`

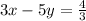
Note that comparing the equations 3x-5y=4 and
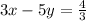`3x-5y=(4)/(3)` the values of a and b are equal but the value of c is different. This means that they have the same slope but a different y-intercept.