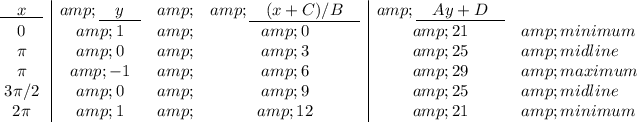Answer: 29 feet (deepest) at 6 am
21 feet (shallowest) at Midnight & Noon
Explanation:
y = -4 cos (π/6)t +25
Amplitude (A) = 4
-A means it is a reflection over the x-axis (starts at minimum)
Period = 2π/B → Period = 12
Phase shift = C/B → Phase Shift = 0
Midline (D) = 25
Midline (D) ± Amplitude (A) = Max & Min
Max: 25 + 4 = 29
Min: 25 - 4 = 21
Change the coordinates of y = cos (x) as follows:
- x-value: Add C then divide by B
- y-value: Multiply by A then add D
Note that the equation shows: A = -4, B = π/6, C = 0, D = 25