Question

A randomized telephone survey of adults in the United States determines that a certain number out of 504 respondents have one or more pets. They use p^ to construct a 95% confidence interval to estimate the proportion p of American adults who have pets to be (0.56137,0.60529).

How many respondents said they have one or more pets?
283
294
305
290

Answer 1

`\hat p=(0.56137+0.60529)/(2)= 0.58333`

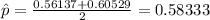
The critical value for 95% of confidence is
`z_(\alpha/2)=1.96`

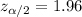
And since we know the total and the proportion is defined as:

`\hat p=(X)/(n)`

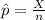
If we solve for X (number of people who say yes) we got:

`X= 0.58333* 504= 293.998 \approx 294`

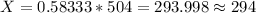
And the best answer would be:

294

Explanation:

We know that the confidence interval for the proportion is given by:

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

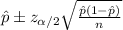
The margin of error for the proportion interval is given by this formula:

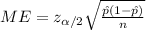`ME=z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}` (a)

The margin of error can be calculated with this formula:

`ME=(0.60529- 0.56137)/(2)= 0.02196`

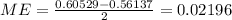
And the estimation for the true proportion is:

`\hat p=(0.56137+0.60529)/(2)= 0.58333`

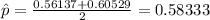
The critical value for 95% of confidence is
`z_(\alpha/2)=1.96`

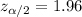
And since we know the total and the proportion is defined as:

`\hat p=(X)/(n)`

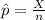
If we solve for X (number of people who say yes) we got:

`X= 0.58333* 504= 293.998 \approx 294`

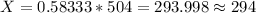
And the best answer would be:

294