Question

Two distinct number cubes, one red and one blue, are rolled together. Each number cube has sides numbered 1 through 6.

What is the probability that the outcome of the roll is an odd sum or a sum that is a multiple of 5?



Enter your answer, in simplest fraction form, in the box.

Answer 1

P=(E1 or E2) 7/12

Explanation:

Answer 2

`P(E_1 or E_2) = (7)/(12)`

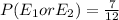
Explanation:

Given

Two cubes of side 1 - 6

Required

Probability that the outcome of the roll is an odd sum or a sum that is a multiple of 5

First, the sample space needs to be listed;

Let
`C_r` represent the Red cube

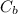`C_b` represent the Blue cube

S represent the sample space

`C_r = (1,2,3,4,5,6)\\C_b = (1,2,3,4,5,6)\\S = (2,3,4,5,6,7,3,4,5,6,7,8,4,5,6,7,8,9,5,6,7,8,9,10,6,7,8,9,10,11,7,8,9,10,11,12)`S is gotten by getting the sum of
`C_r` and
`C_b`

`n(S) = 36`

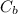
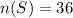
Calculating the Probability

Let
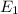`E_1` represent the event that an outcome is an odd sum

`E_1 = (3,5,7,3,5,7,5,7,9,5,7,9,7,9,11,7,9,11)`

`n(E_1) = 18`

`P(E_1) = (n(E_1))/(n(S))`

`P(E_1) = (18)/(36)`

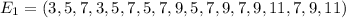
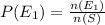
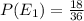
Let
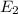`E_2` represent the event that an outcome is a multiple of 5

`E_2 = (5,5,5,5,10,10,10)`

`n(E_2) = 7`

`P(E_2) = (n(E_2))/(n(S))`

`P(E_2) = (7)/(36)`

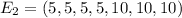
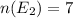
Let
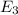`E_3` represent the event that an outcome is an odd sum and a multiple of 5

`E_3 = E_1 and E_2`

`E_3 = (5,5,5,5)`

`n(E_3) = 4`

`P(E_3) = (n(E_3))/(n(S))`

`P(E_3) = (4)/(36)`

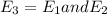
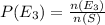
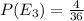
Calculating
`P(E_1 or E_2)`

`P(E_1 or E_2) = P(E_1) + P(E_2) - P(E_1 and E_2)`

`P(E_1 or E_2) = P(E_1) + P(E_2) - P(E_3)`

`P(E_1 or E_2) = (18)/(36) + (7)/(36) - (4)/(36)`

`P(E_1 or E_2) = (18 + 7 - 4)/(36)`

`P(E_1 or E_2) = (21)/(36)`

`P(E_1 or E_2) = (7)/(12)`

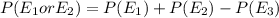
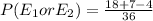
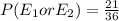
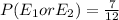
Hence, the probability that the outcome of the roll is an odd sum or a sum that is a multiple of 5 is
`(7)/(12)`