Answer:
a) Null hypothesis:

Alternative hypothesis:
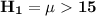
b) the test statistics is : 2.15
c) The p-value is 0.0158
d) NO, there is evidence that the mean time of telephone survey is less than 15 and premium rate is not justified.
Explanation:
The data in the Microsoft Excel are:
17;11;12;23;20;23;15;
16;23;22;18;23;25;14;
12;12;20;18;12;19;11;
11;20;21;11;18;14;13;
13;19; 16;10;22;18;23.
a) Formulate the null and alternative hypotheses for this application.
From the question, Fowle Marketing Research Inc. is taking base charge from a client on the given assumption that if the mean time of telephone survey is 15 minutes or less.
The null and alternative hypotheses are therefore as follows:
Null hypothesis:

The null hypothesis states that there is evidence that the mean time of telephone survey is less than 15 and premium rate is not justified.
Alternative hypothesis:
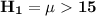
The alternative hypothesis states that there is evidence that the mean time of telephone survey exceeds 15 and premium rate is justified.
b) Compute the value of the test statistic.
Given that:
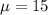
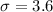
n = 35
The sample mean
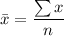 is;
is;
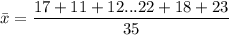
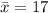
Thus:
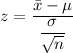
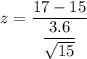
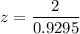
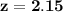
Thus; the test statistics is : 2.15
c) What is the p-value?
p-value = P(Z > 2.15)
p-value = 1 - P(Z ≤ 2.15)
From the standard normal table, the value of P(Z ≤ 2.15) is 0.9842
p-value = 1 - 0.9842
p-value = 0.0158
The p-value is 0.0158
d) At a = .01, what is your conclusion?
According to the rejection rule, if p-value is less than 0.01 then reject null hypothesis at ∝ = 0.01
Thus; p-value = 0.0158 > ∝ = 0.01
By the rejection rule, accept the null hypothesis.
Therefore, there is evidence that the mean time of telephone survey is less than 15 and premium rate is not justified.