Question

The price of fresh, organic blueberries varies over the course of the year. In early July, when blueberries are abundant, a quart of organic blueberries may cost only $4. However, in January, a quart of organic blueberries may cost as much as $9. Model the price of blueberries using a sine or a cosine function. Let x represent the number of months since the beginning of the year(so x=0 means the beginning of January, and x= 6 means the beginning of July). Clearly indicate following:

a. the maximum and minimum
b. the midline
c. the period and rate constant
d. write a formula for the function
e. Clearly label all parts
f. Sketch the graph

May check work by graphing your function on a graphing calculator etc.​

Answer 1

`\bold{\text{Answer:}\quad y=(5)/(2)\cos \bigg((\pi)/(6)x\bigg)+(13)/(2)}`

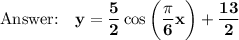
Explanation:

Use the formula y = A cos (Bx - C) + D where

• A = amplitude
• Period = 2π/B
• Phase Shift = C/B
• D = vertical shift (aka midline)

Given: Max = 9, Min = 4, (1/2)Period = 6 → Period = 12

Amplitude (A) = (Max - Min)/2

= (9 - 4)/2

= 5/2

Midline (D) = (Max + Min)/2

= (9 + 4)/2

= 13/2

Period = 2π/B

→ B = 2π/Period

= 2π/12

= π/6

Notice that the Maximum touches the y-axis so there is no phase shift and no reflection → C-value = 0 & A-value is positive

Now, let's put it all together:

A = 5/2, B = π/6, C = 0, D = 13/2

`\large\boxed{y=(5)/(2)\cos \bigg((\pi)/(6)x\bigg)+(13)/(2)}`

Note that your graph will NOT fit the graph given because the max occurs in January (x = 0) and the min occurs in July (x = 6). The graph provided has the min at x = 0 and the max at x = 6.