Question

The index of refraction of Sophia's cornea is 1.387 and that of the aqueous fluid behind the cornea is 1.36. Light is incident from air onto her cornea at an angle of 17.5° from the normal to the surface. At what angle to the normal is the light traveling in the aqueous fluid?

Answer 1

17.85°

Step-by-step explanation:

To find the angle to the normal in which the light travels in the aqueous fluid you use the Snell's law:

`n_1sin\theta_1=n_2sin\theta_2`

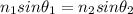
n1: index of refraction of Sophia's cornea = 1.387

n2: index of refraction of aqueous fluid = 1.36

θ1: angle to normal in the first medium = 17.5°

θ2: angle to normal in the second medium

You solve the equation (1) for θ2, next, you replace the values of the rest of the variables:

`\theta_2=sin^(-1)((n_1sin\theta_1)/(n_2))\\\\\theta_2=sin^(-1)(((1.387)(sin17.5\°))/(1.36))=17.85\°`

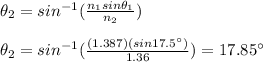
hence, the angle to normal in the aqueous medium is 17.85°