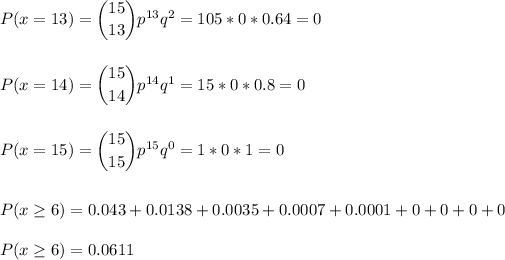Question

. Suppose that only 20% of all drivers come to a complete stop at an intersection having flashing lights in all directions when no other cars are visible. What is the probability that, of 15 randomly chosen drivers coming to an intersection under these conditions,

Answer 1

a. P(x≤9)=0.9999

b. P(x=6)=0.0430

c. P(x≥6)=0.0611

Explanation:

The question is incomplete:

a.At most 9 will come to a complete stop?

b.Exactly 6 will come to a complete stop?

c.At least 6 will come to a complete stop?

d.How many of the next 20 drivers do you expect to come to a complete stop?

The amount of drivers from the sample that will come to a complete stop can be modeled by a binomial random variable with n=15 and p=0.2.

The probability that exactly k drivers from the sample come to a complete stop is:

`P(x=k) = \dbinom{n}{k} p^(k)q^(n-k)`

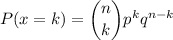
a. We have to calculate the probability that at most 9 come to a complete stop:

`P(x\leq9)=\sum_(k=0)^9P(x=k)\\\\\\P(x=0) = \dbinom{15}{0} p^(0)q^(15)=1*1*0.0352=0.0352\\\\\\P(x=1) = \dbinom{15}{1} p^(1)q^(14)=15*0.2*0.044=0.1319\\\\\\P(x=2) = \dbinom{15}{2} p^(2)q^(13)=105*0.04*0.055=0.2309\\\\\\P(x=3) = \dbinom{15}{3} p^(3)q^(12)=455*0.008*0.0687=0.2501\\\\\\P(x=4) = \dbinom{15}{4} p^(4)q^(11)=1365*0.0016*0.0859=0.1876\\\\\\P(x=5) = \dbinom{15}{5} p^(5)q^(10)=3003*0.0003*0.1074=0.1032\\\\\\P(x=6) = \dbinom{15}{6} p^(6)q^(9)=5005*0.0001*0.1342=0.043\\\\\\`

`P(x=7) = \dbinom{15}{7} p^(7)q^(8)=6435*0*0.1678=0.0138\\\\\\P(x=8) = \dbinom{15}{8} p^(8)q^(7)=6435*0*0.2097=0.0035\\\\\\P(x=9) = \dbinom{15}{9} p^(9)q^(6)=5005*0*0.2621=0.0007\\\\\\P(x\leq9)=0.0352+0.1319+0.2309+0.2501+0.1876+0.1032+0.043+0.0138+0.0035+0.0007\\\\P(x\leq9)=0.9999`

b. We have to calculate the probability that exactly 6 will come to a complete stop:

`P(x=6) = \dbinom{15}{6} p^(6)q^(9)=5005*0.0001*0.1342=0.043\\\\\\`

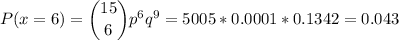
c. We have to calculate the probability that at least 6 will come to a complete stop:

`P(x\geq6)=\sum_(k=6)^(15)P(x=k)\\\\\\P(x=6) = \dbinom{15}{6} p^(6)q^(9)=5005*0.0001*0.1342=0.043\\\\\\P(x=7) = \dbinom{15}{7} p^(7)q^(8)=6435*0*0.1678=0.0138\\\\\\P(x=8) = \dbinom{15}{8} p^(8)q^(7)=6435*0*0.2097=0.0035\\\\\\P(x=9) = \dbinom{15}{9} p^(9)q^(6)=5005*0*0.2621=0.0007\\\\\\P(x=10) = \dbinom{15}{10} p^(10)q^(5)=3003*0*0.3277=0.0001\\\\\\P(x=11) = \dbinom{15}{11} p^(11)q^(4)=1365*0*0.4096=0\\\\\\P(x=12) = \dbinom{15}{12} p^(12)q^(3)=455*0*0.512=0\\\\\\`

`P(x=13) = \dbinom{15}{13} p^(13)q^(2)=105*0*0.64=0\\\\\\P(x=14) = \dbinom{15}{14} p^(14)q^(1)=15*0*0.8=0\\\\\\P(x=15) = \dbinom{15}{15} p^(15)q^(0)=1*0*1=0\\\\\\P(x\geq6)=0.043+0.0138+0.0035+0.0007+0.0001+0+0+0+0\\\\P(x\geq6)=0.0611`