Question

Two samples are randomly selected from each population. The sample statistics are given below.

n1 = 150 n2 = 275
x1 = 72.86 -x2 = 67.34
s1 = 15.98 s2 = 35.67
The value of the standardized test statistic to test the claim that μ1 > μ2 is _________.
-2.19
2.19
3.15
-3.15

Answer 1

Null hypothesis:
`\mu_1 \leq \mu_2`

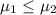
Alternative hypothesis:
`\mu_1 > \mu_2`

The statistic is given by:

`t= \frac{\bar X_1 -\bar X_2}{\sqrt{(s^2_1)/(n_1) +(s^2_2)/(n_2)}}`

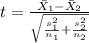
And replacing we got:

`t=\frac{72.86-67.34}{\sqrt{(15.98^2)/(150) +(35.67^2)/(275)}}=2.194`

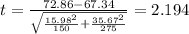
And the best option would be:

2.19

Explanation:

We have the following info given:

n1 = 150 n2 = 275

`\bar x_1 = 72.86, \bar x_2 = 67.34`

s1 = 15.98 s2 = 35.67

We want to test the following hypothesis:

Null hypothesis:
`\mu_1 \leq \mu_2`

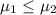
Alternative hypothesis:
`\mu_1 > \mu_2`

The statistic is given by:

`t= \frac{\bar X_1 -\bar X_2}{\sqrt{(s^2_1)/(n_1) +(s^2_2)/(n_2)}}`

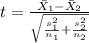
And replacing we got:

`t=\frac{72.86-67.34}{\sqrt{(15.98^2)/(150) +(35.67^2)/(275)}}=2.194`

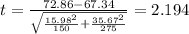
And the best option would be:

2.19