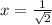Question

Please see attachment

Answer 1

a) The value of absolute minimum value = - 0.3536

b) which is attained at
`x = (1)/(√(2) )`

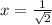
Explanation:

Step(i):-

Given function

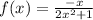`f(x) = (-x)/(2x^(2) +1)` ...(i)

Differentiating equation (i) with respective to 'x'

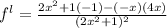`f^(l) = (2x^(2) +1(-1) - (-x) (4x))/((2x^(2)+1)^(2) )` ...(ii)

`f^(l)(x) = (2x^(2)-1)/((2x^(2)+1)^(2) )`

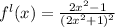
Equating Zero

`f^(l)(x) = (2x^(2)-1)/((2x^(2)+1)^(2) ) = 0`

`(2x^(2)-1)/((2x^(2)+1)^(2) ) = 0`

`2 x^(2)-1 = 0`

`2 x^(2) = 1`

`x^(2) = (1)/(2)`

`x = (-1)/(√(2) ) , x = (1)/(√(2) )`

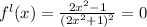
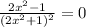
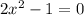
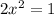
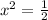
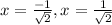
Step(ii):-

Again Differentiating equation (ii) with respective to 'x'

`f^(ll)(x) = ((2x^(2) +1)^(2) (4x) - 2(2x^(2) +1) (4x)(2x^(2)-1) )/((2x^(2)+1)^(4) )`

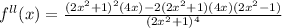
put

`x = (1)/(√(2) )`

`f^(ll) (x) > 0`

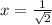
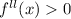
The absolute minimum value at
`x = (1)/(√(2) )`

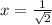
Step(iii):-

The value of absolute minimum value

`f(x) = (-x)/(2x^(2) +1)`

`f((1)/(√(2) ) ) = (-(1)/(√(2) ) )/(2((1)/(√(2) ) )^(2) +1)`

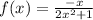
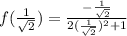
on calculation we get

The value of absolute minimum value = - 0.3536

Final answer:-

a) The value of absolute minimum value = - 0.3536

b) which is attained at
`x = (1)/(√(2) )`