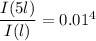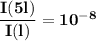Answer:
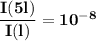
Step-by-step explanation:
We are being told that the current is proportional to the tunneling coefficient
 ;
;
where l = distance between the tip and the surface.
Let
 ------------ equation (1)
------------ equation (1)
and
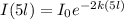 ------------ equation (2)
------------ equation (2)
Dividing equation (2) by (1); we have :
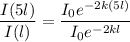
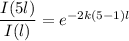

where ;
 represents the transmission coefficient T = 0.01
represents the transmission coefficient T = 0.01
Thus; replacing the value for 0.01;we have;