Question

Element X decays radioactively with a half life of 12 minutes. If there are 760 grams of element X, how long, to the nearest tenth a minute, would it take the element to decay to 15 grams?

Answer 1

The time it'd take for the element to have 15 g of mass is approximately 68 min.

Explanation:

The radioactive decay of a substance is given by the following formula:

`mass(t) = mass(0)*e^(-\lambda*t)`

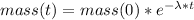
Since the element has a half life of 12 minutes, this means that after this time the mass of the element will be half of it was originally, therefore:

`(mass(0))/(2) = mass(0)*e^(-\lambda*12)`

`(1)/(2) = e^(-\lambda*12)`

`ln((1)/(2)) = -12*\lambda\\\lambda = -(ln(0.5))/(12) =0.0577623`

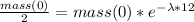
Therefore the mass of the element is given by:

`mass(t) = mass(0)*e^(-0.0577623*t)`

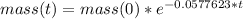
If the initial mass is 760 g and the final mass is 15 g, we have:

`mass(t) = mass(0)*e^(-0.0577623*t)\\\\15 = 760*e^(-0.0577623*t)\\\\e^(-0.0577623*t) = (15)/(760)\\\\ln(e^(-0.0577623*t)) = ln((15)/(760))\\\\-0.0577623*t = ln((15)/(760))\\\\t = (ln((15)/(760)))/(-0.0577623)\\\\t = 67.9555`

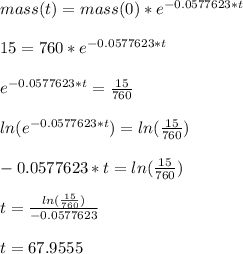
The time it'd take for the element to have 15 g of mass is approximately 68 min.