Question

The relationship between ttt and rrr is expressed by the equation 2t+3r+6=02t+3r+6=02, t, plus, 3, r, plus, 6, equals, 0. If rrr increases by 444, which of the following statements about ttt must be true?

Answer 1

Question:

The relationship between t and r is expressed by the equation 2t+3r+6 = 0. If r increases by 4, which of the following statements about t must be true?

Answer:

The value of t is reduced by 6 when the value of r is increased by 4

Explanation:

Given

`2t + 3r + 6 = 0`

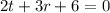
Required

What happens when r is increased by 4

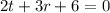`2t + 3r + 6 = 0` -------- Equation 1

Subtract 2t from both sides

`2t + 3r + 6 - 2t = 0 - 2t`

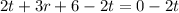
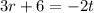`3r + 6 = - 2t` --- Equation 2

When r is increased by 4, equation 1 becomes

`2T + 3(r+4) + 6 = 0`

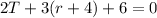
Note that the increment of r also affects the value of t; hence, the new value of t is represented by T

Open bracket

`2T + 3r+12 + 6 = 0`

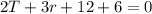
Rearrange

`2T + 3r+6 +12 = 0`

Substitutr -2t for 3r + 6 [From equation 2]

`2T -2t +12 = 0`

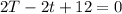
Make T the subject of formula

`2T = 2t - 12`

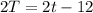
Divide both sides by 2

`(2T)/(2) = (2t - 12)/(2)`

`T = t - 6`

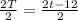
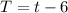
This means that the value of t is reduced by 6 when the value of r is increased by 4