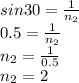Question

:What will be the value of the refractive index of the medium? Critical angle of that medium is 30 degree

a) 2
b) 1.5
c) 1.8
d) 1

Answer 1

Let the second medium be air (n₁=1)

The refractive index n₂ of the medium where first medium is air is found (a)

(a) n₂ = 2

Step-by-step explanation:

Critical angle can be defined as the angle of incidence that provides the angle of refraction of 90°.

Refractive index of a medium can be defined as a number that describes that how fast a light will travel through that medium.

Critical angle and Refractive index are related by:

`\theta_(critical)= sin^(-1)((n_1)/(n_2))`

`sin \theta_(critical)=(n_1)/(n_2)`

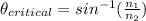
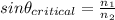
To find refractive index of medium with respect to air, substitute n₁=1 (Refractive index of air is 1)

Also θ(critical)=30°

Find n₂ :

`sin30= (1)/(n_2)\\0.5=(1)/(n_2)\\n_2=(1)/(0.5)\\n_2=2`