Question

The vertex form of a quadratic function is f(x) = a(x - h)2 + k. What is the vertex of each function? Match the function rule with the coordinates of its vertex.

Answer 1

For
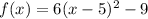`f(x)=6(x-5)^2-9` the vertex is: (5, -9)

For
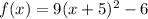`f(x)=9(x+5)^2-6` the vertex is: (-5, -6)

For
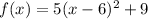`f(x)=5(x-6)^2+9` the vertex is: (6, 9)

For
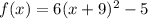`f(x)=6(x+9)^2-5` the vertex is: (-9, -5)

For
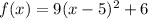`f(x)=9(x-5)^2+6` the vertex is: (5, 6)

Explanation:

Let's identify the vertex pair
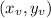`(x_v,y_v)` from each equation:

A)
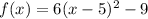`f(x)=6(x-5)^2-9` corresponds to
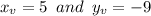`x_v=5\,\,\,and\,\,\,y_v=-9` , that is: (5, -9)

B)
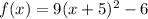`f(x)=9(x+5)^2-6` corresponds to
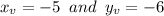`x_v=-5\,\,\,and\,\,\,y_v=-6` , that is: (-5, -6)

C)
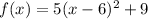`f(x)=5(x-6)^2+9` corresponds to
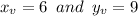`x_v=6\,\,\,and\,\,\,y_v=9` , that is: (6, 9)

D)
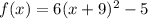`f(x)=6(x+9)^2-5` corresponds to
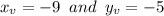`x_v=-9\,\,\,and\,\,\,y_v=-5` , that is: (-9, -5)

E)
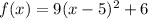`f(x)=9(x-5)^2+6` corresponds to
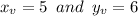`x_v=5\,\,\,and\,\,\,y_v=6` , that is: (5, 6)