Answer:
48 and 4
Explanation:
If we assume that
 to be the random variable that proceed the normal distribution with mean
to be the random variable that proceed the normal distribution with mean
 and a standard deviation
and a standard deviation
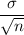
Given that:
mean =48
standard deviation = 16
sample size = 16
The population mean is same as the population mean in sampling distribution that is 48.
The standard deviation of the sampling distribution is therefore calculated as:
standard deviation =
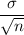
standard deviation =
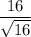
standard deviation =
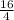
standard deviation = 4
Thus; the mean and the standard deviation of the sampling distribution is 48 and 4