Question

A company that packages peanuts states that at a maximum 6% of the peanut shells contain no nuts. At random, 300 peanuts were selected and 21 of them were empty.

1.With a significance level of 1%, can the statement made by the company be accepted?
2.With the same sample percentage of empty nuts and 1 − α = 0.95, what sample size would be needed to estimate the proportion of nuts with an error of less than 1%?
​

Answer 1

1)
`z=\frac{0.07 -0.06}{\sqrt{(0.06(1-0.06))/(300)}}=0.729`

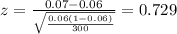
We can calculate the p value with the following formula:

`p_v =2*P(z>0.729)=0.466`

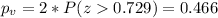
The p value for this case is very high and using the significance level of 0.01 we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the statment makes sense.

2)
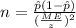`n=(\hat p (1-\hat p))/(((ME)/(z))^2)` (b)

And replacing into equation (b) the values from part a we got:

`n=(0.06(1-0.06))/(((0.01)/(1.96))^2)=2166.66`

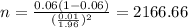
And rounded up we have that n=2167

Explanation:

Information given

n=300 represent the random sample taken

X=21 represent the number of peanuts empty

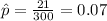`\hat p=(21)/(300)=0.07` estimated proportion of peanust empty

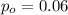`p_o=0.06` is the value to test

`\alpha=0.05` represent the significance level

z would represent the statistic

`p_v` represent the p value

Part 1

We want to test if the true proportion is 6% or no the system of hypothesis are:

Null hypothesis:
`p=0.06`

Alternative hypothesis:
`p \\eq 0.06`

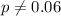
The statistic is given by:

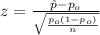`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.07 -0.06}{\sqrt{(0.06(1-0.06))/(300)}}=0.729`

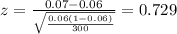
We can calculate the p value with the following formula:

`p_v =2*P(z>0.729)=0.466`

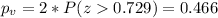
The p value for this case is very high and using the significance level of 0.01 we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the statment makes sense.

Part 2

The margin of error for the proportion interval is given by this formula:

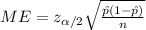`ME=z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}` (a)

And on this case we have that
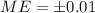`ME =\pm 0.01` and we are interested in order to find the value of n, if we solve n from equation (a) we got:

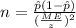`n=(\hat p (1-\hat p))/(((ME)/(z))^2)` (b)

And replacing into equation (b) the values from part a we got:

`n=(0.06(1-0.06))/(((0.01)/(1.96))^2)=2166.66`

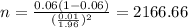
And rounded up we have that n=2167