Question

Question 7

The equation of a straight line AB is

`(x)/(2) + (y)/(2) = 1`

(a) Find the gradient of line AB.
(b) Find the y-intercept of line AB.
(c) A second line PQ is parallel to the line AB and passes through a point (2, -8).
Show that the second line PQ also passes through the point(-1,-5)​

Answer 1

see explanation

Explanation:

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

Given

`(x)/(2)` +
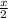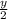`(y)/(2)` = 1 ( multiply through by 2 to clear the fractions )

x + y = 2 ( subtract x from both sides )

y = - x + 2 ← in slope- intercept form

(a) with slope m = - 1

(b) with y- intercept c = 2

(c)

Parallel lines have equal slopes, thus

y = - x + c ← is the partial equation of PQ

To find c substitute (2, - 8) into the partial equation

- 8 = - 2 + c ⇒ c = - 8 + 2 = - 6

y = - x - 6 ← equation of PQ

To show (- 1, - 5) lies on PQ, substitute x = - 1 into the equation and evaluate for y.

y = - (- 1) - 6 = 1 - 6 = - 5 ← the given y- coordinate

Thus PQ passes through (- 1, - 5 )