Answer:
Step-by-step explanation:
a)We find the portfolio weights first. For a two security portfolio
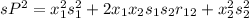
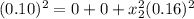
x2 = 0.625 and x1 = 0.375
Then
rp = x1r1 + x2r2
rp = (0.375 ´ 0.06) + (0.625 ´ 0.14)
= 0.11
= 11.0%
Hence, he can improve the expected rate of return without any change in the risk of the portfolio.
b)
The expected return is:
rp = x1r1 + x2r2
rp = (0.5 *´ 0.09) + (0.5 ´* 0.14)
= 0.115 = 11.5%
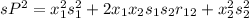
sP2 = (0.5)^2(0.10)^2 + 2*(0.5)(0.5)(0.10)(0.16)(0.10) + (0.5)^2(0.16)^2
sP2 = 0.0097
sP = 0.985 = 9.85%
Hence, he can never perform better by investing equal amount in bond portfolio and index fund. The expected return increases to 11.5% and standard deviation decreases to 9.85%.