Answer:
1. The least squares regression is y = -0.1015·x + 6.51
2. The independent variable is b) age
Please see attached table
Explanation:
The least squares regression formula is given as follows;
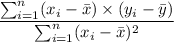
We have;
 = 24
= 24
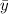 = 4
= 4
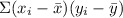 = -79
= -79
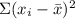 = 778
= 778
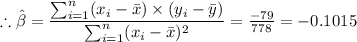
The least squares regression is y = -0.1015·x + α
∴ α = y -0.1015·x = 6 - (-0.1015 × 5) = 6.51
The least squares regression is thus;
y = -0.1015·x + 6.51
2. The independent variable is the age b)
3. Steps to create an ANOVA table with α = 0.05
The overall mean = (43 + 30 + 22 + 20 + 5 + 1 + 6 + 4 + 3 + 6 )/10 = 14
There are 2 different treatment =
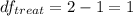
There are 10 different treatment measurement =
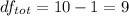
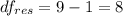
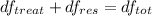
The estimated effects are;

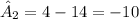
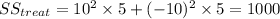
![\sum_(i)\SS_(row)_i = \sum_(i)\sum_(j) (y_(ij) - \bar y)= [(1 - 4)^2 + (6 - 4)^2 + (4 - 4)^2 + (3 - 4)^2 + (6 - 4)^2] = 18](https://img.qammunity.org/2021/formulas/mathematics/college/mvtbudz8iu230m8777cnvpz4o1jgw019tz.png)
![\sum_(i) S S_(row)_i = \sum_(i)\sum_(j) (y_(ij) - \bar y) ^2= [(43 - 24)^2 + (30 - 24)^2 + (22 - 24)^2 + (20 - 24)^2 + (5 - 24)^2] = 778](https://img.qammunity.org/2021/formulas/mathematics/college/s7u0ay7gfhbgd825wzc8kq305yx8ypre4l.png)
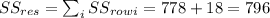
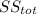 = (43 - 14)² + (30 - 14)² + (22 - 14)² + (20 - 14)² + (5 - 14)² + (1 - 14)1² + (6 - 4 )² + (3 - 14)² + (6 - 14)² = 1796
= (43 - 14)² + (30 - 14)² + (22 - 14)² + (20 - 14)² + (5 - 14)² + (1 - 14)1² + (6 - 4 )² + (3 - 14)² + (6 - 14)² = 1796
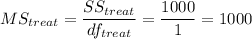
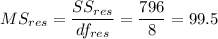
F- value is given by the relation;
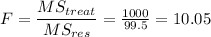
We then look for the critical values at degrees of freedom 1 and 8 at α = 0.05 on the F-distribution tables 5.3177
Hence;
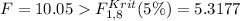 , we reject the null hypothesis.
, we reject the null hypothesis.