Answer:
a) The observational units for this study are coins
b) The test is a two-tailed test.
c) Since the p-value is < α, we can therefore conclude that long-run proportion of heads significantly differ from 0.50
d) The findings are known as statistically important, due to the very large sample size. But the difference between the 0.50 ratio hypothesized and the 0.51 ratio observed isn't very large. Consequently , the findings are not relevant
Explanation:
a) The observational units for this study are coins
b) Number of heads = x = 14709
Number of flips = n = 29015
Sample proportion =
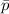 = x ÷ n = 14709 ÷ 29015=0.51
= x ÷ n = 14709 ÷ 29015=0.51
H
 : p =0.50
: p =0.50
H
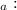 p
p
 0.50
0.50
z =
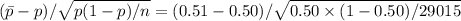
z = 2.366
Using the normal distribution table, area under the normal curve to the right of z;
z = 2.366 = 0.009
The test is a two-tailed test.
Hence, p-value =
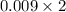 = 0.018
= 0.018
c) α = 0.05
p-value < α = 0.05, we reject the null hypothesis.
We can therefore conclude that long-run proportion of heads significantly differ from 0.50
d) The findings are known as statistically important, due to the very large sample size. But the difference between the 0.50 ratio hypothesized and the 0.51 ratio observed isn't very large. Consequently , the findings are not relevant